Wykres rozrzutu – wprowadzenie
Wykres rozrzutu (ang. scaterplott) jest narzędziem analitycznym, mającym na celu opis i wizualizację związków, korelacji pomiędzy dwiema zmiennymi ciągłymi (Cleveland, McGill, 1984; Friendly, Denis, 2005). Metoda ta jest użyteczna i powszechna w rozmaitych zastosowaniach analitycznych (Spence, Garrison, 1993). Wykorzystanie wykresu rozrzutu do analizy związków wpisuje się także w nurt zarządzania opartego na dowodach (Kulikowski, 2021), którego jednym z elementów jest prowadzenie analizy danych pochodzących z organizacji. W tym tekście skupimy się na praktycznym wprowadzeniu do tworzenia i analizy wykresów rozrzutu oraz omówimy podstawy korzystania z wykresów rozrzutu, tak, by nabyć wiedzę w zakresie ich zastosowania w analityce wynagrodzeń.
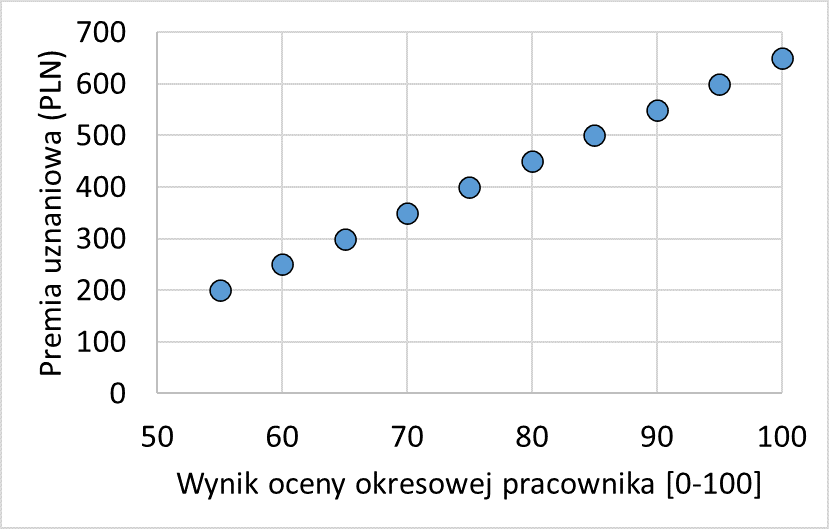
Na początek spróbujmy przyjrzeć się prostemu wykresowi rozrzutu, który może posłużyć nam do omówienia tego, jak działa to narzędzie. Wykres 1 pokazuje przykład standardowo skonstruowanego wykresu rozrzutu. Na osi pionowej (Y) wykresu 1 mamy podane informacje o wysokości przyznanej przez menedżera premii uznaniowej w PLN, a na osi poziomej (X) mamy informacje o wynikach oceny okresowej pracowników. Wiemy także, że najniższy wynik uprawniający do jakiejkolwiek premii to ocena 50. Każdy niebieski punkt na wykresie 1 to zestaw danych, wynik oceny okresowej oraz przypisana mu premia uznaniowa (por. Peng, 2012). Taki wykres można bez trudu stworzyć korzystając z każdego niemal arkusza kalkulacyjnego np. w Excelu, OpenOffice czy LibreOffice jest to wykres punktowy, w arkuszach Google wykres rozproszony.
Wykres rozrzutu ilustrujący pozytywny związek pomiędzy wysokością premii uznaniowej a wynikiem oceny okresowej pracownika
Opracowanie własne Sedlak & Sedlak
Przesuwając się po osi poziomej wykresu 1 w stronę coraz wyższych ocen okresowych, możemy obserwować jak wraz ze zmianą oceny, zmienia się wysokość premii. Widzimy, że osoba, która uzyskała na skali 0-100 ocenę 60, otrzymała 250 PLN premii uznaniowej, a za ocenę 70 wypłacono premię w wysokości 350 PLN. Analiza przedstawionego wykresu rozrzutu pozwala zauważyć, że występuje bardzo silny związek pomiędzy oceną okresową a wysokością przyznanej premii uznaniowej – jest tu bardzo wysoka korelacja pomiędzy zmiennymi. Za każdym razem, gdy ocena pracy rośnie, wzrasta także premia, a punkty na wykresie układają się w linię prostą: im wyższy wynik oceny okresowej, tym wyższa premia. Taka analiza pokazuje, że menedżer postępuje sprawiedliwie: przyznawane przez niego premie rzeczywiście wiążą się z jakością pracy, bo wyższe premie otrzymują ci pracownicy, którzy uzyskali wyższe oceny (ale przecież nie zawsze musi tak być, o czym za chwilę).
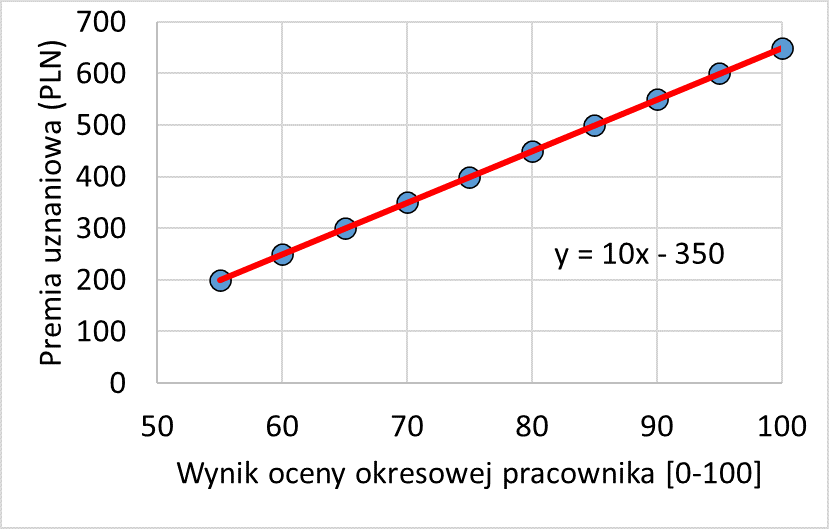
Dodatkową praktyczną korzyścią z wykresu rozrzutu jest to, że do zbioru punktów widocznych na wykresie, możemy dopasować linię trendu, która opisana będzie wzorem pozwalającym nam lepiej zrozumieć siłę związku między oceną i premią oraz da możliwość, by przedstawić ten związek w formie matematycznej formuły. Linia trendu to linia, która jest poprowadzona w taki sposób, by była jak najlepiej dopasowana do wszystkich punktów na wykresie, czyli by jej odchylenie od punktów wykresu było jak najmniejsze. Jeśli punkty na wykresie układają się na linii prostej, to najlepiej dopasowaną linią trendu będzie właśnie linia prosta, przechodząca przez ich środek. Linia taka dopasowana jest na wykresie 2.
Wykres rozrzutu ilustrujący związek pozytywny pomiędzy wysokością premii uznaniowej a wynikiem oceny okresowej pracownika z dopasowaną linią trendu opisaną wzorem
Opracowanie własne Sedlak & Sedlak
Na wykresie 2 możemy zobaczyć czerwoną linię trendu dopasowaną do punktów oraz opisujący ją wzór matematyczny w formie y = 10x – 350. Przypomnijmy, że na naszym wykresie Y to wartość na osi pionowej, czyli wysokość premii uznaniowej, a X to wartość na osi poziomej, czyli ocena okresowa. Zatem dzięki ustaleniu dla naszego wykresu rozrzutu wzoru y = 10x – 350, zyskujemy dwie ważne w praktyce informacje.
Po pierwsze, z analizy naszego równania możemy ocenić, jak silnie ocena pracy powiązana jest z premią uznaniową. Ponieważ wzór zawiera formułę 10 * X, możemy zauważyć, że wzrost wartości X o jedną jednostkę, czyli wzrost oceny, którą otrzymał pracownik o jeden punkt, wiąże się z 10-złotowym wzrostem premii uznaniowej. Z kolei, jeśli ocena pracy (czyli X) wzrośnie o 10 punktów, to premia uznaniowa wzrośnie o 10 * X = 10 * 10 = 100 PLN. Dzięki tym informacjom pochodzącym z matematycznego wzoru opisującego linię trendu, możemy w praktyce określić jak silnie powiązane są zmienne na wykresie rozrzutu. W naszym przypadku wiemy jak silnie ocena okresowa powiązana jest z premią przyznawaną przez menedżera, czyli jaką wagę premiujący przykłada do ocen okresowych, gdy ustala premie.
Drugą ważną korzyścią, jaka płynie z posiadania równania opisującego związek pomiędzy oceną okresową a premią uznaniową, to możliwości przewidywania premii na podstawie znajomości oceny. Przykładowo: na wykresie rozrzutu widzimy, że żaden z pracowników nie otrzymał oceny 87 punktów, ale mając ustalony nasz algorytm opisujący linię trendu, możemy próbować wyliczyć, jaką premię otrzymałby taki pracownik. Wystarczy tu do wzoru opisującego nasz związek y = 10x - 350, za X podstawić żądaną wartość oceny okresowej, a zatem mamy y = 10 * 87 - 350 = 870 - 350 = 520. Wiemy zatem, że gdyby menedżer stosował cały czas te same kryteria premiowania, jak na naszym wykresie 2, to za ocenę 87 powinien przyznać premię w wysokości 520 PLN. Innymi słowy, wzór y = 10x – 350, to w naszym przypadku wzór na wysokość premii uznaniowej, algorytm premiowania. Taki wzór, jeśli uznamy go za odpowiedni dla potrzeb premiowania, możemy także przekazać innym menedżerom, by z niego korzystali.
Trzecią ważną w praktyce wartością liczbową, jaką możemy uzyskać z wykresu rozrzutu jest współczynnik determinacji R2, który mówi nam o tym, jak dobrze nasza linia trendu dopasowana jest do danych na wykresie. Współczynnik determinacji R2 może przyjmować wartości od 0% do 100%, gdzie 0% to najgorsze możliwe dopasowanie, a 100% najlepsze możliwe dopasowanie do danych. W naszym przypadku linia trendu przechodzi idealnie przez środek wszystkich punktów na wykresie, zatem linia ta jest idealnie dopasowana do punktów, a współczynnik determinacji wynosi 100%. Nasze przewidywania wysokości premii na podstawie wzoru dopasowanego do wykresu rozrzutu są całkowicie zgodne z rzeczywistymi wysokościami premii (jednak nie zawsze sytuacja będzie tak idealna, jak w naszym przykładzie). Współczynnik determinacji możemy także interpretować jako procent zmienności jednej zmiennej wyjaśnianej przez zmienność drugiej zmiennej. Gdy znamy już ideę wykresu rozrzutu i rozumiemy, jak go stosować w praktyce, przejdźmy do przykładu bardziej złożonego, zaprezentowanego na wykresie 3.
Wykres rozrzutu ilustrujący brak związku pomiędzy wysokością premii uznaniowej a wynikiem oceny okresowej pracownika
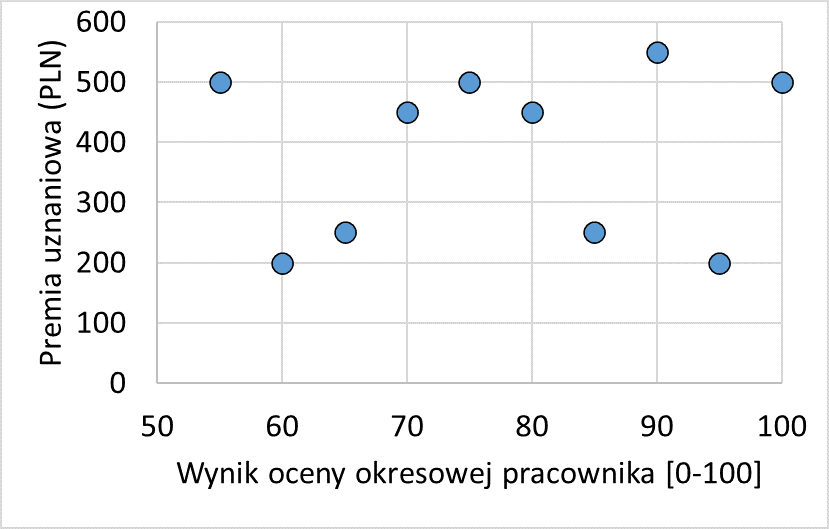
Opracowanie własne Sedlak & Sedlak
Na wykresie 3, tak jak poprzednio na wykresach 1 i 2, na osi poziomej (X) przedstawiamy wynik oceny okresowej, a na osi pionowej (Y) przyznaną premię uznaniową. Tym razem punkty na wykresie nie układają się w jedną linię prostą, ale są rozrzucone po całym jego obszarze. Jeśli przyjrzymy się danym na wykresie to zauważymy, że pracownik, który uzyskał ocenę pracy równą 55 punktów otrzymał premię 500 PLN, taką samą, jak ten, który uzyskał ocenę 100 punktów. Pracownicy, którzy uzyskali oceną 70 i 80 otrzymali takie same premie w wysokości 450 PLN. Jeden z pracowników, który otrzymał bardzo wysoką ocenę okresową równą 95 punktów na 100, dostał tylko 200 PLN premii. Analizując wykres 3 widzimy, że pomiędzy wysokością premii a oceną okresową nie ma w praktyce żadnego związku. Gdy zmienia się ocena to premia uznaniowa ani systematycznie nie rośnie ani też nie spada, ale zmienia się w zupełnie przypadkowy sposób, a między tymi dwiema zmiennymi nie ma korelacji. Wydaje się zatem, że menedżer, który przyznawał premie nie radzi sobie z wyznaczaniem adekwatnych sum, gdyż ustalane przez niego wysokości premii nie są w żaden sposób powiązane z jakością pracy. Do punktów na wykresie 3, tak jak do tych na wykresie 2, również możemy spróbować dopasować linię prostą, tak by przebiegała jednocześnie jak najbliżej wszystkich punktów. Ponieważ punkty są nierównomiernie rozrzucone, nie da się poprowadzić linii prostej, która przechodziłaby przez wszystkie punkty, tak jak zrobiliśmy to na wykresie 2. Wciąż możemy jednak, korzystając z wbudowanych w arkusze kalkulacyjne algorytmów, obliczyć przebieg linii trendu tak, by ta była możliwie jak najbliżej każdego z punktów. Taką najlepiej dopasowaną linię dla wykresu 3 wraz z równaniem, które ją opisuje, prezentujemy na wykresie 4.
Wykres rozrzutu ilustrujący brak związku pomiędzy wysokością premii uznaniowej a wynikiem oceny okresowej pracownika z dopasowaną linią trendu opisaną wzorem
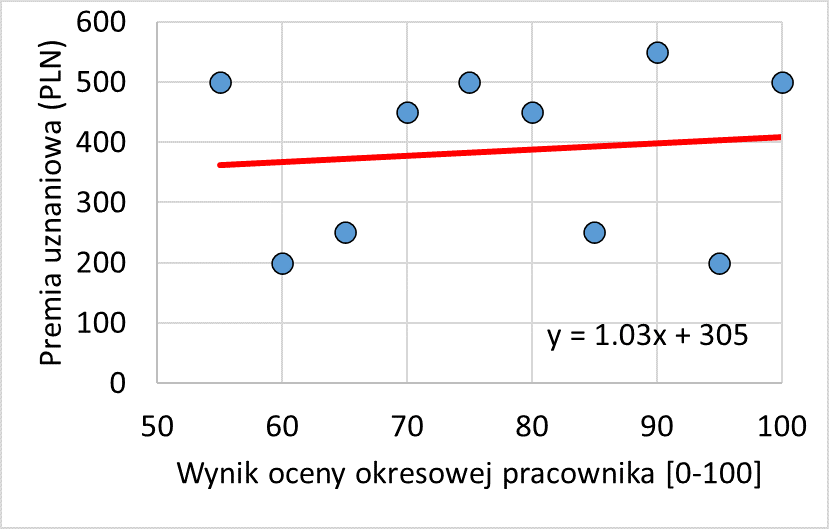
Opracowanie własne Sedlak & Sedlak
Punkty na wykresie 4 są mocno rozrzucone dokoła wyznaczonej linii trendu, więc już na pierwszy rzut oka widzimy, że związek między premią a oceną okresową jest bardzo słaby i nieregularny. Jeśli przyjrzymy się wzorowi opisującemu linię trendu, który ma postać: y = 1.03*x + 305, zobaczymy także, że przewiduje on, iż wzrost oceny okresowej o jedną jednostkę, będzie wiązał się ze wzrostem premii o 1 PLN. Zatem dla danych na wykresie 4, premia uznaniowa, jaką menedżer przyznaje, bardzo słabo wiąże się z oceną okresową, jaką pracownicy uzyskali. Jeśli ocena okresowa wzrośnie o 10 punktów, to nasz wzór przewiduje zmianę premii jedynie o 10 PLN. Spróbujmy teraz dokonać obliczeń premii dla oceny równej 90, korzystamy z ustalonego wcześniej wzoru: y = 1.03*x +305, za x podstawiamy 90 i otrzymujemy y = 1.03 * 90 + 305 = 92.7 + 305 = 397.7. Nasze równanie przewiduje, że dla osoby o ocenie 90, premia wyniesie ok. 400 PLN, gdy w rzeczywistości osoba to otrzymała 500 PLN. Nie jest to zatem przewidywanie zbyt trafne. Dodatkowo, jeśli dla danych na wykresie rozrzutu 4 policzymy współczynnik determinacji R2, uzyskamy wartość 1%, co wskazuje na to, że linia trendu jest bardzo słabo dopasowana do naszych danych i korzystanie z opisującego ją wzoru jest bardzo ryzykowne. I nie ma w tym nic specjalnie dziwnego, skoro premia okresowa i ocena nie są wyraźnie powiązane, to trudno oczekiwać, by na podstawie oceny dało się przewidzieć wysokość premii.
W naszym przykładzie wykres 4 ewidentnie pokazuje, że pomiędzy oceną okresową a premią uznaniową nie ma żadnego wyraźnego związku. Można stąd wyciągnąć ważny praktyczny wniosek, że menedżer kieruje się w przyznawaniu premii innymi kryteriami niż wynik oceny okresowej, może uznaje ocenę za niewiarygodną, a może premiuje tych, których lubi niezależnie od tego jak pracują? Analiza wykresu rozrzutu w analityce wynagrodzeń dostarcza nam cennych i użytecznych informacji. Jeśli założymy, że wykres 2 oraz wykres 4, to wykresy dla dwóch różnych menedżerów, odpowiednio A i B, to na podstawie tej analizy możemy dokonać benchmarku, porównać i ocenić sprawiedliwość przyznawanych przez nich premii. Co więcej, nie tylko możemy ocenić sprawiedliwość ocen, ale także możemy zaradzić niskiej rzetelności menedżera B. Możemy zaproponować, by zamiast bazować na swoich odczuciach i intuicjach, skorzystał z algorytmu premiowania, który udało nam się wyekstrahować z tego, w jaki sposób premiuje rzetelny menedżer A.
Podsumowanie
Omówiliśmy, czym jest wykres rozrzutu i jak w praktyce można z niego korzystać analizując dane o wynagrodzeniach. Przeprowadzone dotychczas analizy, choć relatywnie proste, to pokazują szereg konkretnych praktycznych zastosowań wykresu rozrzutu w analityce wynagrodzeń. Wykres ten pozwala ilustrować związki między wynagrodzeniem a innymi zmiennymi oraz opisywać ten związek linią trendu wraz z odpowiednim matematycznym algorytmem. Omówione przykłady były uproszczone, a wykres rozrzutu ma dziesiątki innych zastosowań (por. Sarikaya, Gleicher, 2017), ale głównym celem naszych przykładów jest ilustracja tego, jak budując systemy wynagradzania skutecznie stosować wykres rozrzutu. To proste narzędzie analityki wynagrodzeń, kiedy nauczymy się z niego właściwie korzystać, możemy stosować do wielu różnych praktycznych problemów – czy premia wiąże się z efektywnością pracy?, czy oceny menedżerów powiązane są z wynikami pracy?, jak wprowadzenie nowych składników wynagradzania wiąże się z produktywnością? Te i inne pytania dotyczą związków między wynagrodzeniem a innymi zmiennymi. Na takie pytania możemy próbować odpowiedzieć korzystając z możliwości, jakie daje nam wykres rozrzutu, narzędzie dostępne w każdym arkuszu kalkulacyjnym. W świecie zdominowanym przez informacje, umiejętność wizualizacji danych jest tak samo ważna jak umiejętność czytania i pisania. Kto tego nie rozumie może stać się współczesnym analfabetą (Börner, Bueckle, Ginda, 2019).