Jak znaleźć punkt odniesienia w analityce wynagrodzeń – czyli percentyle jako narzędzie analizy struktury wynagrodzeń

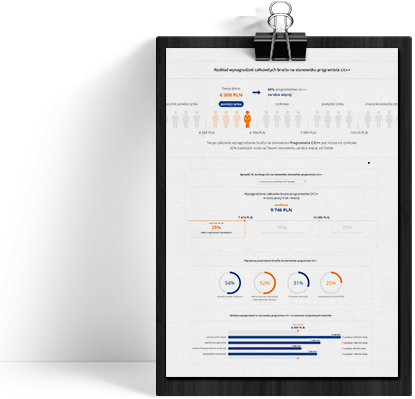
Analizując wynagrodzenia, szczególnie istotne jest przyglądanie się nie tylko wartościom bezwzględnym, ale także analiza wynagrodzeń w oparciu o jasny punkt odniesienia. Przykładowo, sama informacja, że Jan Nowak dostał 500 PLN premii nic nam nie mówi o tym, czy to premia wysoka czy niska i jakie na taką premię mogą być reakcje Nowaka i jego współpracowników. Jednak już informacja, że Nowak dostał premię 500 PLN, a 75% pracowników dostało premie niższe od niego, pozwala nam zyskać punkt odniesienia. Mając taki punkt odniesienia, widzimy, że premia Nowaka była wysoka na tle innych, co od razu skłania do zastanowienia, czy tak wysoka premia idzie w parze z równie wysokimi wynikami pracy. Podobnie, gdy pracownicy oceniają sprawiedliwość własnego wynagrodzenia, często szukają punktu odniesienia w postaci wynagrodzenia współpracowników czy stawek u konkurencji. Choć mogą znaleźć się tacy, którzy stwierdzą, że nie potrzebują punktów odniesienia, bo sami wiedzą, ile powinni zarabiać, to dla wielu pracowników punkt odniesienia jest potrzebny, by wiedzieć, czy zarabiają dużo czy mało.

Podobnie jest w analityce wynagrodzeń. Czy 4000 PLN to dużo czy mało? Informacja, że przeciętne wynagrodzenie pracowników produkcji wynosi 4000 PLN, niewiele mówi nam o konkurencyjności wynagrodzenia w naszej firmie, jeśli nie wiemy jakie są przeciętne wynagrodzenia pracowników produkcji w naszym regionie. W praktycznej analityce wynagrodzeń ważne jest nie tylko wyliczanie wskaźników, ale posiadanie punktu porównawczego dla ich wartości. Wiedzą o tym specjaliści wynagradzania posługujący się w swoich analizach medianą – czyli wartością środkową. Przypomnijmy, że mediana to wartość, która dzieli analizowany zbiór wynagrodzeń na dwie równe części, np. dla wynagrodzeń 3000; 4000; 5000; 6000; 7000, mediana to wartość środkowa - 5000 PLN. Jeśli wiem, że mediana wynagrodzeń pracowników produkcji w mojej firmie wynosi 4000 PLN, a mediana wynagrodzeń pracowników produkcji w moim regionie wynosi 5000 PLN, to widzę, że inni płacą lepiej niż my. Nie możemy oceniać wynagrodzeń tylko w odniesieniu do osobistych przekonań zarządu czy menedżerów, np. że 4000 PLN to bardzo dużo dla pracownika produkcji i więcej nie zapłacimy. Dopiero mając punkt odniesienia możemy określić, jaka kwota to „dużo”, a jaka „mało”. Na rynku pracy wygrywa nie ten, kto opiera się na swoich przekonaniach o tym, jakie powinny być wynagrodzenia, ale ten, kto wie, jakie wynagrodzenia rzeczywiście są i potrafi tę wiedzę wykorzystać.

Mediana to często wykorzystywany punkt odniesienia w analizach wynagrodzenia, pozwalający opierać się na tym jak jest, a nie na tym jak chcielibyśmy, żeby było. Ma ona wiele zalet, np. jest mniej niż średnia arytmetyczna wrażliwa na obserwacje odstające, ale nie jest miarą doskonałą, a jej zalety mogą niekiedy stawać się wadami. Mediana będąc odporną na wartości skrajne, może nie pozwalać na wychwycenie zróżnicowania struktury wynagrodzeń. Dlatego analiza mediany, jako jedynego punktu odniesienia w analityce wynagrodzeń, może być niewystarczająca a nawet myląca.

Przyjrzyjmy się wyzwaniom, jakie mogą wynikać z bazowania tylko na medianie w analityce wynagrodzenia. Przypuśćmy, że, aby ustalić ile powinniśmy płacić naszym pracownikom produkcji, porównujemy medianę wynagrodzeń na stanowisku technika produkcji w naszej firmie i u konkurencji, w obu przypadkach mediana wynagrodzeń wyniosła 4000 PLN. Czy możemy stwierdzić, że wynagrodzenia w obu przypadkach są takie same, a my płacimy tak jak konkurencja? Niestety nie, mediana informuje nas tylko o tym, jaki jest punkt środkowy, wartość 4000 PLN dzieli wynagrodzenia w obu firmach na połowy, ale nie wiemy nic o tym, co dzieje się w obrębie tych połówek. Zilustrujmy to prostym przykładem. Dla zbioru wynagrodzeń: 1000 PLN, 4000 PLN, 10 000 PLN, wartość środkowa - mediana wynosi 4000 PLN, ale taka sama jest mediana dla zbioru trzech zupełnie innych wynagrodzeń: 3500 PLN, 4000 PLN, 4500 PLN. Dla obu grup wartość środkowa - mediana to 4000 PLN, ale nie powiemy tu chyba, że oba zbiory przedstawiają takie same wynagrodzenia. To, że wartość środkowa jest taka sama, nie oznacza jeszcze, że struktura wynagrodzeń jest porównywalna. Podobnie może być w omawianym wcześniej przypadku, w naszej firmie i u konkurencji mediany mogą być identyczne, np. 4000 PLN, ale struktura wynagrodzeń może być zupełnie inna. Zatem samo opieranie się na medianie może być mylące. Co zrobić, by poprawić wynik analizy danych i nie wpadać w pułapki pochopnych konkluzji opartych o medianę? Powinniśmy odwoływać się nie tylko do mediany, ale też do percentyli!

Ujmując rzecz precyzyjnie, w zbiorze danych od X1 do XY ułożonych od najmniejszej do największej, w którym liczba dystynktywnych elementów jest równa y, n-ty percentyl to wartość, od której mniejszych jest n% obserwacji. Jeśli liczba dystynktywnych elementów jest mniejsza niż y, wówczas n-ty percentyl to wartość, od której mniejszych lub równych jest n% obserwacji (por. Lee, 1986; Walter, 1986). By unikań nadmiernego teoretyzowania, dla uproszczenia załóżmy, że percentyl powinien informować nas, jaki procent obserwacji w zbiorze ma mniejszą wartość niż wartość tego percentyla (por. NIST/SEMATECH e-Handbook of Statistical Methods, 2022; Frost, 2022). Czyli, jeśli 25 percentyl dla wypłaconych wynagrodzeń wynosi 3500 PLN, oznacza to, że 25% obserwacji (pracowników) otrzymało wynagrodzenie niższe niż 3500 PLN. Oczywiście zależność ta będzie spełniona tylko w dużych zbiorach danych, w małych zbiorach liczenie percentyli może dawać jedynie wyniki przybliżone i często może być bezużyteczne, np. liczenie 25 percentyla dla zbioru 5 liczb może być zadaniem dość karkołomnym. Przykładowo, w zbiorze 1000; 2000; 3000; 4000; 5000, 25 percentylowi policzonemu w programie Excel funkcją PERCENTYL.PRZEDZ.OTW, odpowiada 1500 PLN. W zbiorze danych od 1500 PLN mniejsza jest tylko 1 obserwacja, co więcej, wartość 1500 PLN jest wartością estymowaną, nie ma jej w zbiorze danych.

Przypomnijmy jeszcze raz, że w uproszczeniu, mediana to wartość, która dzieli zbiór interesujących nas wynagrodzeń na połowy, tak, że 50% pracowników zarabia mniej niż mediana. Zatem mediana odpowiada 50 percentylowi i, jak widać, percentyle to „miary” precyzyjniejsze niż mediana. Opisowo możemy powiedzieć, że o ile mediana dzieli dany zbiór wynagrodzeń na dwie części, to percentyle dzielą go na sto równych części (oczywiście zbiór musi być odpowiednio liczny). Od wartości mediany, czyli 50 percentyla, 50% wartości w zbiorze jest mniejszych. Z kolei wartość przypisana do 25 percentyla to wartość, od której mniejszych jest 25% wynagrodzeń w danym zbiorze, a wartość 75 percentyla, to wartość, od której mniejszych jest 75% wynagrodzeń w analizowanym zbiorze.

Możemy wyznaczyć nie tylko 50, 25 czy 75 percentyl, ale dowolne percentyle jakie przyjdą nam do głowy, np. 66 lub 39, jednak analitycy często odwołują się do 25 i 75 percentyla. Wydaje się, że percentyle te są szczególnie interesujące, ponieważ pozwalają ocenić, co dzieje się na „początku” i „końcu” zbioru analizowanych wartości. Przykładowo w dwóch firmach produkcyjnych A i B, mediana wynagrodzeń może być identyczna i wynieść 4000 PLN, ale w firmie A 75 percentyl ma wartość 5000 PLN, a w firmie B 75 percentyl ma wartość 10 000 PLN. Oznacza to, że mimo iż w obu firmach połowa pracowników zarabia mniej niż 4000 PLN, to w firmie A 75% pracowników zarabia mniej niż 5000 PLN, natomiast w firmie B 75% pracowników zarabia mniej niż 10 000 PLN. Wskazuje to na zupełnie inną, nieporównywalną strukturę wynagrodzeń w tych firmach. W tym wypadku, wiedza o tym, jaki jest 75 percentyl pozwala nam ocenić, co dzieje się w obrębie górnej „połówki” wyznaczonej przez medianę. W firmie A nawet wynagrodzenia wysokie na tle tego zakładu pracy, są skupione dokoła mediany, w firmie B wynagrodzenia wysokie oddalają się od mediany. W praktyce może to sugerować, iż w firmie A kładzie się nacisk na to, by wynagrodzenia najlepszych i przeciętnych pracowników były porównywalne, a w firmie B akcentuje się to, by wynagrodzenie najlepszych pracowników było znacznie wyższe niż pracowników przeciętnych. Taka analiza uwzględniająca wartość 75 percentyla dostarcza nam o wiele więcej informacji niż informacja, że w obu firmach A i B mediana jest równa 4000 PLN, co mogłoby skłaniać do pochopnej konkluzji, że obie firmy wynagradzają pracowników w dokładnie ten sam sposób.

Podsumowując, możemy w zasadzie dowolnie wyznaczać percentyle w zakresie liczb całkowitych od 1 do 100, jednak w praktyce, taka dowolność powodowałaby chaos i sporo nieporozumień. Jedni analitycy mogliby odwoływać się w swoich raportach do 70 percentyla, inni do 60, a jeszcze inni 80. Dlatego, by dokonać systematyzacji w analizach biorących pod uwagę percentyle, skupiamy się zwykle w pierwszej kolejności na wyznaczeniu 25 i 75 percentyla. Wartości te są często wykorzystywane w analizach danych i, tak jak 50 percentyl uzyskał nazwę mediany, tak 25 i 75 percentyl, również mają swoje nazwy, 25 percentyl nazywany jest pierwszym kwartylem, a 75 percentyl trzecim kwartylem. Jeśli wyznaczymy percentyle co 25%, to podzielą one zbiór obserwacji na 4 części. Graficzną uproszczoną ilustrację związku między medianą i kwartylami przedstawia rysunek 1. Patrząc na rysunek 1 możemy także zauważyć, że pierwszy kwartyl jest medianą pierwszej połowy obserwacji, a trzeci kwartyl jest medianą drugiej połowy obserwacji.

By uniknąć pochopnego interpretowania danych o wynagrodzeniach na podstawie mediany, powinniśmy analizować nie tylko medianę - punkt, który dzieli zbiór wynagrodzeń na połowy (50 percentyl), ale też to, jakie są punkty, które dzielą zbiór wynagrodzeń w taki sposób, że mniejszych od nich jest 25% wynagrodzeń (25 percentyl) lub 75% wynagrodzeń (75 percentyl). Punkty te, nazwane odpowiednio pierwszym i trzecim kwartylem, oznaczamy Q1 i Q3. Uzupełniając medianę kwartylami dokonujemy bardziej precyzyjnego opisu naszego zbioru wynagrodzeń i możemy lepiej zrozumieć, jak poszczególne wynagrodzenia wypadają na tle innych.

Dodatkowo wyznaczenie pierwszego i trzeciego kwartyla (25 i 75 percentyla), pozwala na pokazanie rozstępu międzykwartylowego, oznaczanego skrótem IQR (interquartile range). Ponieważ wskaźnik ten w języku polskim może mieć różne określenia, np.: rozstęp kwartylowy lub przedział międzykwartylowy, dla jasności będziemy posługiwać się pochodzącym z angielskiego skrótem IQR. Wskaźnik IQR obliczamy jako różnicę pomiędzy trzecim kwartylem (75 percentylem) a pierwszym kwartylem (25 percentylem). Opisuje on zakres, w którym znajduje się 50% wynagrodzeń położonych centralnie w zbiorze danych.
Zobaczmy, jakich informacji w praktyce dostarcza wskaźnik IQR w analityce wynagrodzeń. W naszym wcześniejszym przykładzie dwóch firm produkcyjnych A i B mediana wynagrodzeń wynosiła 4000 PLN, ale w firmie A, 75 percentyl miał wartość 5000 PLN, a w firmie B 10 000 PLN, dodajmy jeszcze, że w firmie A 25 percentyl wynosił 2000 PLN, a w firmie B 3000 PLN. Dane te zaprezentowane zostały w tabeli 1. 

Wskaźnik IQR (trzeci kwartyl - pierwszy kwartyl) dla firmy A wynosi 5000 PLN – 2000 PLN = 3000 PLN, a dla firmy B 10 000 PLN - 3000 PLN = 7000 PLN. O ile dla firm znajdujących się w tabeli 1 mediana jest identyczna, to wskaźniki IQR znacząco się różnią, pokazując rozpiętość wynagrodzeń w środkowej części danych. W praktycznych zmaganiach z analityką wynagrodzeń, pozwala to nam zdobyć lepszy wgląd w strukturę wynagrodzeń w obu firmach.

Gdy w analityce wynagrodzeń w celu zdobycia punktu odniesienia odwołujemy się do mediany, zawsze gdy to tylko możliwe uzupełniajmy nasze analizy o wartości percentyli. Jako standard warto podawać pierwszy i trzeci kwartyl, czyli 25 i 75 percentyl. Pozwoli to unikać pochopnych wniosków i nietrafionych porównań.